Soal dan Pembahasan Tentang Peluang

• Rumus umum aturan faktorial.

n! = n x (n – 1) x (n – 2) x (n – 3)!

• Rumus umum Permutasi.

nPr = n!/(n – r)!

• Rumus umum Permutasi Melingkar.

(n-1)!

• Rumus umum Kombinasi

nCr = n!/(r!(n – r)!)

• Rumus umum Peluang

P = n(A)/n(S)

Berikut beberapa contoh - contoh soalnya :

1. Nilai n yang memenuhi untuk nP5 = 9. (n-1)P4 ?

Penyelesaian:

Jadi nilai n = 9.

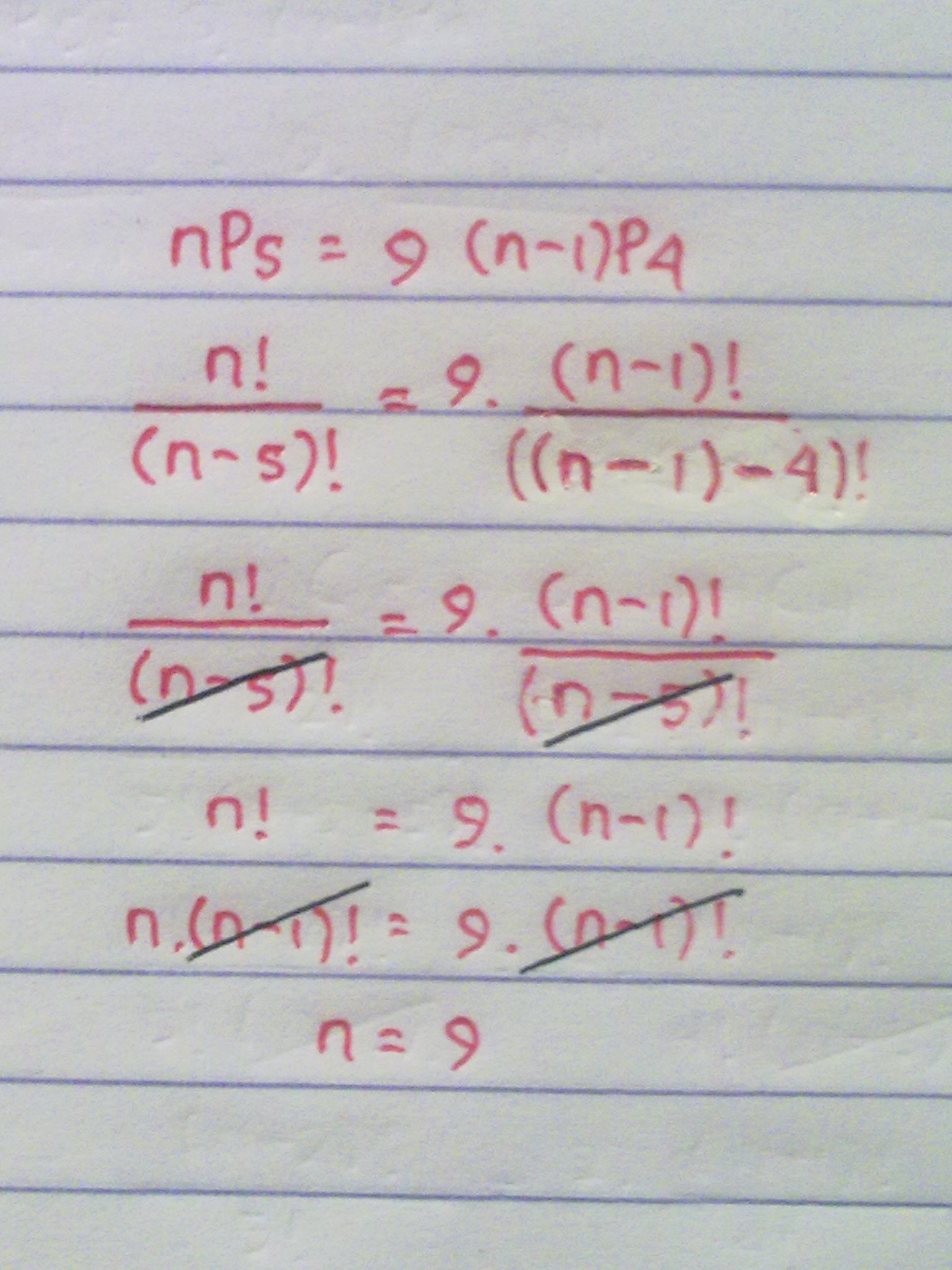
2. Jika (n+2)C5 = 2. (n+1)C4. Maka nilai dari 2n + 3 adalah…

Penyelesaian:

Didapat nilai n = 8. Jadi nilai 2n + 3 = 2.8 + 3 = 19.


3. Buktikan mengapa 0! = 1 ?

Penyelesaian:
Seperti yang kita tahu, misalnya:

4! = 4x3x2x1

6! = 6x5x4x3x2x1

1! = 1.

Dengan beberapa contoh ini dapat disimpulkan bahwa:

n! = n x (n – 1)!

Kemudian kita dapat bagi setiap sisi dengan n.

n!/n = [n x (n – 1)!]/n

n!/n = (n – 1)!

Nah kemudian coba subtitusi nilai n = 1. Maka:

n!/n = (n – 1)!

1!/1 = (1 – 1)!

1 = 0!

0! = 1 —–> terbukti.


4. Ada 9 bola.Tiap bola ditandai dengan angka yang saling berlainan yakni: mulai dari 12, 13, 14, 15, 16, 17, 18, 19 dan 20. Dilakukan pengambilan 2 bola secara acak. Tentukan peluang munculnya 2 bola dengan jumlah angka yang genap?

Penyelesaian:
Jumlah sampel = 9.

12, 13, 14, 15, 16, 17, 18, 19, 20

Genap = 5

Ganjil = 4

2 buah angka yang dijumlahkan hasilnya GENAP, jika:
GENAP + GENAP = GENAP
GANJIL + GANJIL = GENAP.


Banyaknya cara munculnya angka GENAP + GENAP

= 5C2 = 5!/2!.3! = 10 cara.

Banyaknya cara munculnya angka GANJIL + GANJIL

= 4C2 = 4!/2!.2! = 6 cara.

Jadi, peluang munculnya 2 angka dengan jumlah genap adalah:

P = n(A)/n(S)

P = [5C2 + 4C2] / 9C2

P = [10 + 6] / 9C2


untuk 9C2 = 9!/2!.7!

= 9.8.7!/2.7!

= 72/2 = 36.

Maka,

P = [10 + 6] / 9C2

P = [10 + 6]/36

P 16/36 = 4/9.


5. Terdapat 3 mata uang logam yang dilemparkan bersamaan. Tentukan besar frekuensi harapan peluang munculnya sisi muka lebih dari satu pada 64 percobaan pelemparan?

Penyelesaian:
Mis: S = sisi muka uang logam

B = sisi belakang uang logam.

Banyaknya kejadian/sampel yang muncul saat terjadi pelemparan 3 mata uang logam bersamaan, ada pada gambar di bawah ini;



Jumlah kejadian/sampel = 8.

Dimana 4 diantaranya adalah kejadian dimana sisi muka muncul lebih dari satu, yakni: MMM, MMB, MBM, BMM.

Peluang munculnya sisi muka lebih dari satu adalah

P = n(A)/n(S)

P = 4/8 = 1/2.

Jadi, frekuensi harapannya adalah

= n.P = 64. 1/2 = 32.